How To Find Acceleration On Velocity Time Graph

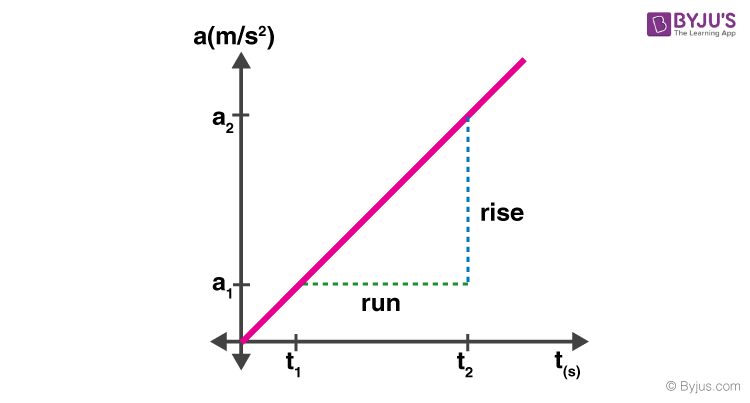
The slope of the acceleration graph represents a quantity known equally a jerk. Jerk is the rate of alter of acceleration. In the given acceleration graph as shown below, the slope tin exist calculated as follows:

\(slope=\frac{rising}{run}=\frac{a_{2}-a_{1}}{t_{2}-t_{1}}=\frac{\Delta a}{\Delta t}\)

Slope of Acceleration Graph

Area Under the Acceleration Graph

The surface area under the acceleration graph represents the change in velocity. In other words, the area nether the graph for a certain time interval is equal to the modify in velocity during that time interval.

\(Area=\Delta V\)

Let us consider the below instance to understand better:

The graph beneath shows a constant acceleration of 4 thousand/s² for a time of ix s.

Acceleration is defined every bit,

\(\Delta a=\frac{\Delta v}{\Delta t}\)

By multiplying both sides of the equation by change in time \(\Delta t\), we get

\(\Delta 5=a\Delta t\)

Substituting the values in the to a higher place equation, nosotros get

\(\Delta v=a\Delta t=(iv\,m/s^ii)(ix\,s)=36\,yard/due south\)

Multiplying the acceleration past the time interval is equivalent to finding the expanse nether the curve.

The area nether the curve is a rectangle. This area can exist found by multiplying height and width.

The elevation, in this case, is four m/sⁱⁱ and the width is nine s.

\(expanse=4\,m/s^2\times 9\,south=36\,grand/s\)

The area under any dispatch graph for a certain time interval gives the change in velocity for that time interval.

Acceleration Graph Solved Example

A racecar driver is cruising at a constant velocity of xx thousand/s. Every bit she nears the finish line, the race auto driver starts to accelerate. The graph shown below gives the acceleration of the race auto as it starts to speed up. Presume the race motorcar had a velocity of 20 m/s at time t=0 due south. Observe the last velocity of the driver when she reaches the terminate line.
Acceleration Time Graph

Solution:

Nosotros tin can notice the change in velocity by finding the surface area under the dispatch graph.

\(\Delta five = area=\frac{one}{2})(8\,southward)(six\,m/s^ii)=24\,thou/s\)

Substituting the values, we get

\(\Delta v = surface area=\frac{one}{ii})(8\,due south)(vi\,thou/s^2)=24\,m/s\)

This calculation gave u.s.a. the change in velocity during the given fourth dimension interval. To summate the final velocity, we demand to use the definition of change in velocity.

\(\Delta five=v_{f}-v_i\)

Substituting the values in the equation, nosotros get

\(v_{f}-twenty\,1000/southward=24\,g/due south\)

\(v_f=44\,m/south\)

Therefore, the concluding velocity of the racer is 44 yard/south.

Lookout the video and acquire the velocity-time graph and displacement-time graph in detail. Past the stop of this video, you lot volition learn what do the slope of the displacement-time graph and velocity-fourth dimension graph signify.

Oftentimes Asked Questions – FAQs

What is Dispatch-Time Graph?

Acceleration-Fourth dimension Graph is a graph that shows the dispatch plotted against time for a particle moving in a straight line.

What does an Acceleration-Time graph tell usa?

Dispatch-fourth dimension graphs tell usa about an object's velocity the same fashion velocity vs time graphs tell us nigh an object'southward deportation.