How To Find The Maximum Of A Quadratic
FIND THE MAXIMUM AND MINIMUM VALUE OF QUADRATIC FUNCTION
The graph of a quadratic function volition always be a parabola which is either open upward or downward.
General course of quadratic function is
f(10) = ax2 + bx + c
Maximum Value of a Quadratic Function
The quadratic function f(x) = ax2 + bx + c will have only the maximum value when the the leading coefficient or the sign of 'a' is negative.
When 'a' is negative the graph of the quadratic office will exist a parabola which opens down.
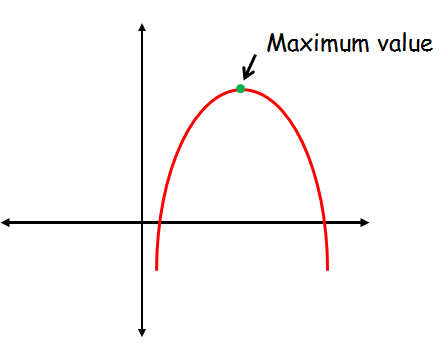
The maximum value is 'y' coordinate at the vertex of the parabola.
Note :
At that place is no minimum value for the parabola which opens downward.
Minimum Value of a Quadratic Function
The quadratic function f(10) = axtwo + bx + c will accept only the minimum value when the the leading coefficient or the sign of 'a' is positive.
When 'a' is positive, the graph of the quadratic part volition exist a parabola which opens up.
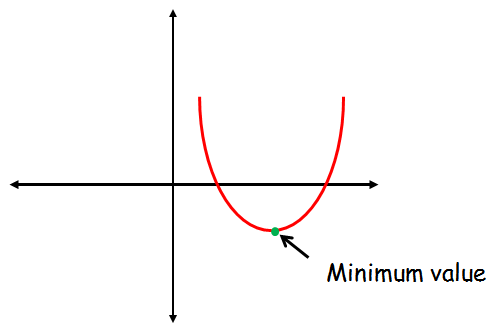
The minimum value is 'y' coordinate at the vertex of the parabola.
Note :
There is no maximum value for the parabola which opens upward.
Solved Bug
Problem 1 :
Find the minimum or maximum value of the quadratic function given below.
f(10) = 2xii + 7x + five
Solution :
Because the coefficient of ten2 is positive, the parabola is open up upwardly.
So, the function will accept only the minimum value and the minimum value is y-coordinate of the vertex.
To find the y-coordinate of the vertex, first we have to notice the x-coordinate of the vertex.
Formula to find x-coordinate of the vertex is
= -b/2a
Substitute a = 2 and b = seven.
= -seven / 2(2)
= -7/iv
To find the y-coordinate of the vertex, substitute -7/4 for x in the given function.
y-coordinate is
= f(-7/4)
= two(-seven/4)2 + 7(-7/4) + five
= 2(49/16) - (49/4) + 5
= (49/eight) - (49/4) + 5
= (49 - 98 + 40)/8
= -9/8
The minimum value is -nine/8.
Problem two :
Find the minimum or maximum value of the quadratic office given below.
f(x) = -2x2 + 6x + 12
Solution :
Because the coefficient of x2 is negative, the parabola is open downward.
So, the function will have merely the maximum value and the maximum value is y-coordinate of the vertex.
To observe the y-coordinate of the vertex, first nosotros have to find the x-coordinate of the vertex.
Formula to detect x-coordinate of the vertex is
= -b/2a
Substitute a = -2 and b = 6.
= -vi/ii(-2)
= -6/(-4)
= 3/2
To detect the y-coordinate of the vertex, substitute 3/ii for x in the given function.
y-coordinate is
= f(3/2)
= -2(3/ii)2 + half dozen(three/2) + 12
= -2(9/4) + iii(iii) + 12
= -9/2 + nine + 12
= -9/2 + 21
= (-ix + 42)/2
= 33/ii
The maximum value is 33/2.
Trouble 3 :
Notice the minimum or maximum value of the quadratic part given below.
f(10) = -5x2 + 30x + 200
Solution :
Because the coefficient of xii is negative, the parabola is open downward.
So, the part will have only the maximum value and the maximum value is y-coordinate of the vertex.
To observe the y-coordinate of the vertex, starting time we have to find the x-coordinate of the vertex.
Formula to find x-coordinate of the vertex is
= -b/2a
Substitute a = -five and b = 30.
= -30/2(-5)
= -thirty/(-10)
= 3
To find the y-coordinate of the vertex, substitute 3 for ten in the given function.
y-coordinate is
= f(3)
= -5(3)2 + 30(iii) + 200
= -5(9) + 90 + 200
= -45 + 290
= 245
The maximum value is 245.
Problem iv :
Find the minimum or maximum value of the quadratic function given below.
f(ten) = 3x2 + 4x + 3
Solution :
Because the coefficient of xii is positive, the parabola is open up upwards.
So, the role will have only the minimum value and the minimum value is y-coordinate of the vertex.
To find the y-coordinate of the vertex, first we have to notice the x-coordinate of the vertex.
Formula to discover x-coordinate of the vertex is
= -b/2a
Substitute a = 3 and b = four.
= -4/2(3)
= -2/3
To find the y-coordinate of the vertex, substitute -2/3 for 10 in the given function.
y-coordinate is
= f(-2/three)
= 3(-ii/3) 2 + 4(-2/3) + 3
= 3(4/9) - 8/3 + 3
= four/3 - 8/3 + 3
= (four - 8)/3 + three
= -iv/3 + 3
= -iv/3 + 9/iii
= (-4 + nine)/3
= 5/3
The minimum value is 5/3.

Autonomously from the stuff given above, if you need whatsoever other stuff in math, delight utilize our google custom search here.
Kindly postal service your feedback tov4formath@gmail.com
We always appreciate your feedback.
© All rights reserved. onlinemath4all.com
Source: https://www.onlinemath4all.com/find-the-maximum-and-minimum-value-of-quadratic-function.html
Posted by: frazierliblow.blogspot.com


0 Response to "How To Find The Maximum Of A Quadratic"
Post a Comment